Makalah FISIKA Tumbukan Impuls dan Momentum

MAKALAH FISIKA DASAR

TUMBUKAN, IMPULS, DAN MOMENTUM

 

1.1 Latar Belakang Masalah

Nilai - nilai selalu berada di setiap kegiatan kita, tanpa kita sadari kegiatan kita sehari-hari juga memanfaatkan system kerja rumus fisika. Pada kesempatan ini akan kami bahas mengenai kegunaan teori momentum. Sebelum kita membahas apa kegunaan momentum terlebih dahulu kita mempelajari apa yang di maksud dengan momentum.

Ketika terjadi suatu kecelakaan di jalan tabrakan antara ke dua buah kendaraan yang berbeda kecepatan, dimana kendaraan yang benrkepatan tinggi mengalami kerusakan yang lebih parah di bandingkan dengan kendaraan yang berkecepatan rendah. Hal ini bisa terjadi, karena semakin besar massa dan kecepatan yag dimiliki benda bergerak maka semakin sulit untuk dihentikan dan makin besar akibatnya.

Kalau kita tinjau dari ilmu fisika, fatal atau tidaknya tabrakan antara kedua kendaraan ditentukan oleh momentum kendaraan tersebut. Dalam ilmu fisika terdapat dua jenis momentum yaitu momentum sudut dan momentum linier. Momentum linier biasanya disebut momentum. Maka momentum adalah hasil kali massa dan kecepatan.

1.2 Rumusan Masalah

a)      Apakah yang dimaksud dengan momentum?

b)      Bagaimana hubungan momentum dan impuls?

c)      Bagaimana mamfaat hukum momentum dalam kehidupan sehari-hari?

d)     Bagaimana menganalis peristiwa tumbukan sesuai hukum kekekalan momentum?

e)      Bagaimana mengaplikasi hukum momentum dalam kehidupan sehari-hari?

1.3 Tujuan Penulisan

a)      Untuk mengetahui dan memahami apa yang dimaksud dengan momentum.

b)      Dapat memaparkan hubungan momentum dan impuls

c)      Dapat memanfaatkan hukum momentum dalam kehidupan sehari-hari.

d)     Dapat menganalisis peristiwa tumbukan sesuai hukum kekekalan momentum

e)      Dapat mengaplikasikan hukum momentum dalam kehidupan sehari-hari.

BAB II

PEMBAHASAN

2.1       PUSAT MASSA (PM)

Dalam gerak translasi, tiap titik pada benda mengalami pergeseran yang sama dengan titik lainnya sepanjang waktu, sehingga gerak dari salah satu partikel dapat menggambarkan gerak seluruh benda. Tetapi, walaupun di dalam geraknya, benda juga berotasi atau bervibrasi, akan ada satu titik pada benda yang bergerak serupa dengan gerak partikel, titik tersebut disebut pusat massa.

Ini merupakan salah satu contoh gerak umum. Gerak umum adalah suatu jenis gerak dimana benda tidak melakukan gerak translisi murni. Dengan kata lain tidak semua bagian benda bergerak dengan lintasan yang sama

Perhatikan pergerakan tongkat diatas. Tongkat melakukan gerak rotasi sepanjang arah horizontal (ke kanan). Ketika berotasi, posisi tongkat selalu berubah-ubah. Walaupun demikian, terdapat satu bagin tongkat yang bergerak sepanjang lintasan lurus yang diberi garis putus-putus, bagian pada tongkat ditandai dengan titik hitam. Bagian tongkat yang diberi tanda titik hitam itu adalah pusat massa tongkat.

Dapat disimpulkan, pusat massa dan titik berat suatu benda memiliki pengertian yang sama, yaitu suatu titik tempat berpusatnya massa/berat dari benda tersebut. Perbedaannya adalah letak pusat massa suatu benda tidak dipengaruhi oleh medan gravitasi, sehingga letaknya tidak selalu berhimpit dengan letak titik beratnya.

Pusat Massa (PM) adalah titik di mana gaya neto dianggap bekerja pada benda tersebut,untuk tujuan menentukan gerak translasi benda secara keseluruhan. Komponen x dari  pusat massa untuk sebuah system yang terdiri dari benda-benda bermassa  m_A, M_b, …, dirumuskan sebagai berikut:

X_PM=  m_Ax_A+m_Bx_B+…. 

m_A+m_B +….

Pusat massa system bermassa total M bergerak dalam lintasan yang sama yang akan ditempuh partikel  M jika mendapat gaya eksternal yang sama. Dalam bentuk persamaan,hal ini merupakan hukum kedua Newton untuk system partikel :

M a_PM = F _neto

Di mana M adalah massa total system, a_CM   adalah gaya eksternal neto yang bekerja pada seluruh bagian system.

2.2       GERAK PUSAT MASSA

Terdapat sekumpulan partikel dengan massa masing-masing : m₁, m₂ , ... ,  m_n dengan massa total M. Dari teori pusat massa diperoleh :

                                    M r_pm = m₁r₁ + m₂r₂ + ...  + m_n r_n

dengan r_pm adalah pusat massa susunan partikel tersebut.

Bila persamaan tersebut dideferensialkan  terhadap waktu t, diperoleh

                                    M dr_pm /dt= m₁ dr₁/dt + m₂  dr₂/dt + ...  + m_n dr_n/dt

                                    M v_pm = m₁v₁ + m₂v₂ + ...  + m_n v_n

Bila dideferensialkan sekali lagi, diperoleh

                                    M dv_pm /dt= m₁ dv₁/dt + m₂  dv₂/dt + ...  + m_n dv_n/dt

                                    M a_pm = m₁ a₁ + m₂ a₂ + ...  + m_n a_n

Menurut hukum Newton, F = m a, maka F₁ = m₁ a₁,  F₂= m₂ a₂    dst.

                                          

                                                                                

2.3       MOMENTUM LINEAR

Di dalam fisika, dikenal dua macam momentum, yaitu momentum linear (p) dan momentum sudut (L).Kadang-kadang momentum linear disingkat momentum. Jangan bingung Ketika  membaca buku pelajaran fisika yang hanya menulis “momentum”. Yang dimaksudkan buku itu adalah momentum linear.Seperti pada gerak lurus, kita seringkali hanya menyebut kecepatan linear dengan “kecepatan”.Tetapi yang kita maksudkan sebenarnya adalah “kecepatan linear”.Momentum linear merupakan momentum yang dimiliki benda-benda yang bergerak pada lintasan lurus, sedangkan momentum sudut dimiliki benda-benda yang bergerak pada lintasan melingkar.

Momentum suatu benda yang bergerak adalah hasil perkalian antara massa benda dan kecepatannya. Oleh karena itu, setiap benda yang bergerak memiliki momentum. Secara matematis, momentum linear ditulis sebagai berikut:

p = m v                 

padalah momentum (besaran vektor), m massa (besaran skalar) dan vkecepatan (besaran vektor). Bila dilihat persamaan (1), arah dari momentum selalu searah dengan arah kecepatannya.

Menurut Sistem Internasional (SI),

Satuan momentum p   = satuan massa x satuan kecepatan

= kg x m/s

= kg .m/s

Jadi, satuan momentum dalam SI adalah : kg.m/s

Momentum adalah besaran vektor, oleh karena itu jika ada beberapa vektor momentum dijumlahkan, harus dijumlahkan secara vektor. Misalkan ada dua buah vektor momentum p₁ dan p₂ membentuk sudut α, maka jumlah momentum kedua vektor harus dijumlahkan secara vektor,

Momentum dan Impuls dalam pemebahasan fisika adalah sebagai satu kesatuankarena Momentum dan Impuls dua besaran yang setara. Dua besaran dikatakan setara seperti Momentum dan Impuls bila memiliki satuan Sistem Internasional (SI) sama atau juga dimensi sama seperti yang sudah dibahas dalam besaran dan satuan.Momentum merupakan sebagai ukuran kesungkaran sesuatu benda di gerakan maupun di berhentikan.momentum sering disebut sebagai jumlah gerak. Momentum suatu benda yang bergerak didefinisikan sebagai hasil perkalian antara massa dengan kecepatanbenda. Secara matematis dirumuskan:

P = m .v

Keterangan

● p : momentum (kg m/s)

●  m : massa benda (kg)

●  v : kecepatan benda (m/s)

Jika kita perhatikan persamaan di atas maka kita dapat menentukan jenis besaran momentum.Massa m merupakan besaran skalar dan kecepatan v adalah besaran vektor, berarti momentum merupakan besaran vektor.Dimana arah p searah dengan arah vektor kecepata Jadi momentum adalah besaran yang dimiliki oleh sebuah benda atau partikel yang bergerak.

2.4       IMPULS

Impuls adalah peristiwa gaya yang bekerja pada benda dalam waktu hanya sesaat. Atau Impuls adalah peristiwa bekerjanya gaya dalam waktu yang sangat singkat. Contoh dar kejadian impuls adalah: peristiwa seperti bola ditendang, bola tenis dipukul karena pada saat tendangan dan pukkulan, gaya yang bekerja sangat singkat.

Impuls didefinisikan sebagai hasil kali gaya dengan waktu yang dibutuhkan gaya tersebut bekerja. Dari definisi ini dapat dirumuskan seperti berikut :

I = F . ∆t

Keterangan: I = impuls (Ns)

                     F = gaya (N)

      ∆t = waktu (s)

            Impuls merupakan besaran vektor.Pengertian impuls biasanya dipakai dalam peristiwa besar di mana F >> dan t <<. Jika gaya F tidak tetap (F fungsi dari waktu), maka rumus I=F.t tidak berlaku. Impuls dapat dihitung juga dengan cara menghitung luas kurva dari grafik F vs waktu

2.5       IMPULS SAMA DENGAN PERUBAHAN MOMENTUM

Suatu partikel yang bermassa m bekerja gaya F yang konstan, maka setelah waktu ∆t partikel tersebut bergerak dengan kecepatan Vt = Vo + a ∆t seperti halnya materi GLBB (gerak lurus berubah beraturan).Sebuah benda bermassa m mula-mula bergerak dengan kecepatan v₁ dan kemudian pada benda bekerja gaya sebesar Fsearah kecepatan awal selama Δt, dan kecepatan benda menjadi v₂.

Untuk menjabarkan hubungan antara Impuls dengan perubahan momentum, akan kita ambil arah gerak mula-mula sebagai arah positif dengan menggunakan Hukum Newton II.

F = m a

= m (v₂ – v₁) Δt

FΔt    = mv₂ – mv₁

Ruas kiri merupakan impuls gaya dan ruas kanan menunjukkan perubahan momentum. Impuls gaya pada suatu benda sama dengan perubahan momentum benda tersebut. Secara matematis dituliskan sebagai:

FΔt   = m v₂ - m v₁

   I     = p₂ - p₁

   I     = Δp

2.6       HUKUM KEKEKALAN MOMENTUM  LINEAR

            Hukum kekakalan momentum menyatakan bahwa “jika tidak ada gaya luar yang bekerja pada sistem, maka momentum total sesaat sebelum sama dengan momentum total sesudah tumbukan”. ketika menggunakan persamaan ini, kita harus memerhatikan arah kecepatan tiap benda.

Contoh aplikasi dari hukum kekekalan momentum adalah roket dan pistol. Pada Gambar 5.3 tampak sebuah pistol yang digantung pada seutas tali. Saat peluru ditembakkan ke kanan dengan alat jarak jauh seperti remote, senapan akan tertolak ke kiri. Percepatan yang diterima oleh pistol ini berasal dari gaya reaksi peluru pada pistol (hukum III Newton).

Contoh aplikasi yang lain adalah pada sistem roket. Percepatan roket diperoleh dengan cara yang mirip dengan bagaimana senapan memperoleh percepatan. Percepatan roket berasal dari tolakan gas yang disemburkan roket. Tiap molekul gas dapat dianggap sebagai peluru kecil yang ditembakkan roket. Jika gaya gravitasi diabaikan, maka peristiwa peluncuran roket memenuhi hukum kekekalan momentum.

Mula-mula sistem roket diam, sehingga momentumnya nol. Sesudah gas menyembur keluar dari ekor roket, momentum sistem tetap. Artinya momentum sebelum dan sesudah gas keluar sama. Berdasarkan hukum kekekalan momentum, besarnya kelajuan roket tergantung banyaknya bahan bakar yang digunakan dan besar kelajuan semburan gas. Hal inilah yang menyebabkan wahana roket dibuat bertahap banyak.

Penerapan hukum kekekalan momentum linear pada roket

2.7       TUMBUKAN DAN JENIS TUMBUKAN

Tumbuhan atau lentingan bisa dikatakan juga sebagai pantulan, karna terjadi pada dua buah benda yang saling berpadu dan memantul akibat dari paduan tersebut. Pada pembahasan kali ini kita akan mempelajari tumbukan yang paling sederhana, yaitu Tumbukan Sentral. Tumbukan sentral adalah tumbukan yang terjadi bila titik pusat benda yang satu menuju ke titik pusat benda yang lain.

Peristiwa tumbukan antara dua buah benda dapat keduanya bergerak saling menjahui. Ketika benda tersebut mempuyai kecepatan dan massa, maka benda itu pasti memilki momentum (p = m .v) dan juga Energi kinetik (EK = ½ m . v²). Tumbukan dibedakan menjadi beberapa jenis:

1.      Tumbukan lenting sempurna

2.      Tumbukan lenting sebagian

3.      Tumbukan tidak lenting sama sekali

Perbedaan tumbukan-tumbukan tersebut dapat diketahui bedasarkan nilai koefisien tumbukan (koefisien restitusi) dari dua benda yang bertumbukan.

Dengan : e = koefisien rrestitusi (0 ≤ e ≥1)

Nilai koefisien restitusi mulai dari 0 hingga 1. Dengan ketentuan:

·         Lenting Sempurna e = 1

·         Lenting Sebagian 0 < e < 1

·         Tidak Lenting Sama Sekali e = 0

1.         Tumbukan lenting sempurna

Dua buah benda dikatakan lenting sempurna, apabila dalam tumbukan tersebut tidak kehilangan energi kinetik. Jadi, energi kinetik sesudah dan sebelum tumbukan adalah tetap. Pada tumbukan lenting sempurna berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik. Berlakunya  hukum kekekalan energi kinetik karena total massa dan kecepatan kedua benda sama, baik sesudah maupun sebelum tumbukan. Dengan persamaan sebagai berikut:

a.   Kekekalan Momentum

 

b.   Kekekalan energi kinetik

Ek₁ + Ek₂ = Ek^’₁ + Ek^’₂

1/2 m₁ v₁² + 1//2 m₂ v₂² = 1/2 m₁ (v^’₁)² + 1/2 m₂ (v^’₂)²

c.    Dengan demikian, pada tumbukan lenting sempurna koefisien restitusi (e)= 1

Nilai koefisien elastisitas / koefisien restitusi (e) pada tumbukan lenting sempurna berlaku:

 

2.         Tumbukan lenting sebagian

Ketika kita menjatuhkan sebuah bola karet dari ketinggian tertentu di atas lantai, maka bola akan memantul. Setelah mencapai titik tertinggi, bola aka jatuh lagi dan memantul lagi setelah mengenai lantai. Begitu seterusnya hingga bola akhirnya berhenti. Hal yang perlu kita perhatikan adalah ketinggian maksimal yang dicapai pada setiap tahap pemantulan selalu berbeda. Pada pemantulan pertama, bola mencapai titik tertinggi yang lebih rendah dari pantulan pertama begitu seterusnya.

Kenyataan ini memberikan arti bahwa kecepatan bola sebelum menumbuk lantai lebih besar dari kecepatan bola setelah tumbukan. Sehingga koefisien restitusi pada kejadian ini berkisar antara nol sampai satu (0< e < 1). Tumbukan seperti ini disebut tumbukan lenting sebagian atau tumbukan elastis sebagian.

Pada peristiwa pemantulan bola pada lantai, energi kinetik yang dimiliki bola tidak tetap. Ini dapat dilihat dari kecepatan bola yang berubah sebelum dan sesudah tumbukan. Jadi, hukum kekekalan energi kinetik pada tumbukan lenting tidak berlaku. Akan tetapi, hukum kekekalan energi mekanik tetap berlaku. Hal ini disebabkan karena sebagian energi kinetik yang hilang telah diubah menjadi bentuk lainya, seperti energi potensial, energi panas, atau energi yang merusak lantai.

Pada kasus bola yang dijatuhkan dari ketinggian h, sehingga dipantulkan dengan ketinggian h^‟, maka memiliki nilai koefisien elastisitas sebesar:

 

keterangan: h’= tinggi pantulan benda

h = tinggi benda semula / tinggi pantulan sebelumnya

3.         Tumbukan tidak lenting sam sekali

 

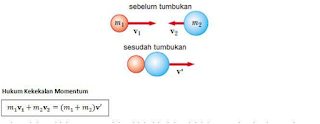
Tumbukan tidak elastis sama sekali terjadi apabila dua benda setelah tumbukan menjadi satu dan bergerak bersama-sama. Contoh sederhana dari tumbukan tidak elsatis sama sekali adalah tumbukan dua bola yang akhirnya bergabung menjadi satu yang akhirnya bergerak bersama dengan kecepatan yang sama pula. Kejadian ini dapat dijelaskan dengan hukum kekekalan momentum.

Dari persamaan di ata, kecepatan bola dapat dicari dengan mudah jika kecepatan bola keduanya semula diketahui, karena kecepatan bola keduanya setelah tumbukan sama, maka koefisien restitusi untuk tumbukan tidak lenting sama sekali adalah nol(0).

Pada tumbukan tidak lenting sama sekali tidak berlaku hukum kekekalan enrgi kinetik. Pada tumbukan ini terjadi pengurangan enrgi kinetik sehingga energi kinetik total benda-benda setelah terjadi tumbukan akan lebih kecil dari energi kinetik total benda sebelum. Dengan demikian:

 

2.8 CONTOH SOAL

Contoh soal pada youtube bisa diakses berikut ini:

 

Contoh soal momentum

Ada sebuah benda yaitu benda A bermassa 2 kg, bergerak kekanan dengan kelajuan 10 m/s. Benda B yang bermassa 7 kg bergerak kekiri dengan kelajuan 4 m/s. Tentukan:

·         Momentum benda A

·         Momentum benda B

·         Momentum total benda A dan B

Penyelesaian :

Diketahui:       Benda A          → m = 2 kg

V = 10 m/s

                        Benda B          → m = 7 kg

V = 4 m/s

Momentum benda A :  P = m . v

                                        = 2 . 10

                                        = 20 Ns

Momentum benda B :  P = m . v

                                        = 7.4

                                    = 28 Ns

Momentum total benda A dan B : 20Ns + 28Ns = 48

2. Nama : Loranza Afrianti

Contoh soal impuls

Sebuah benda diam yang memiliki massa 500 g, setelah mendapat gaya, kecepatannya 25 m/s.Berapa besar impuls tersebut?

Jawab:

Diketahui:       m = 500 g → 0,5 kg

V₂ = 25 m/s

V₁ = 0 m/s

                Ditanya:           I    = …… ?

I   = m (V₂-V₁)

                                            =0,5(25-0)

                                            =12,5 Ns

Contoh Soal Pusat Massa

Sebuah tongkat homogen tipis dengan panjang L berdiri seimbang vertikal diatas lantai yang licin. Pada tongkat tersebut diberi gaya yang amat kecil disembarang titik sepanjang tongkat buakan pada arah vertikal sehingga tongkat tersebut terjatuh. Berapakah perpindahan horizontal titik pusat massanya?

Penyelesaian

Ditanya perpindahan horizontal titik pusat massanya. Karena lantai licin dan gaya yang mengenai tongkat dianggap amat kecil, maka gaya yang bekerja pada tongkat tersebut hanyalah gaya berat tongkat mg pada titik pusat massa P dan gaya normal lantai pada tongkat, yaitu N, Misalkan tongkat di beri gaya pada titik A diatas pusat massa, karena tidak ada gaya arah horizontal maka gaya berat dari pusat massa akan berarah lurus ke titik O tanpa bergeser, sehingga dapat disimpulkan bahwa pergeseran pusat massa adalah 0.

Contoh soal tumbukan

Bola A dan bola B bergerak di atas bidang datar segaris kerja. Bola A dengan massa 2 kg bergerak ke kanan dengan kecepatan 4 m/s dan bola B dengan massa 1 kg bergerak ke kiri dengan kecepatan 6 m/s. Kedua bola bertumbukan sentral. Hitunglah kecepatan masing-masing bola setelah tumbukan jika tumbukan kedua bola:
a. tidak lenting sama sekali
b. lenting sebagian dengan e = 0,8
c. lenting sempurna

Contoh soal pusat massa

Dua silinder homogen disusun seporos dengan panjang dan massanya masing-masing: l₁ = 5 cm ; m₁ = 6 kg ; l₂ = 10 cm ; m₂ = 4 kg.
Tentukan letak titik berat sistem silinder tersebut !

Jawab:

Kita ambil ujung kiri sebagai acuan, maka:

x₁ = 0.5 . l₁ = 2.5 cm

x₂ = l₂ + 0.5 . l₁ = 5 + 5 = 10 cm

X = (å m_i . x_i)/(m_i)
X = (m₁.x₁) + (m₁.x₁)/(m₁ + m₂)

X = (6 . 2.5 + 4 . 10)/(6 + 4)
X = (15 + 40)/(10) = 5.5 cm

Jadi titik beratnya terletak 5.5 cm di kanan ujung m₁

Contoh soal momentumDan impuls

 Sebuah bola dengan massa 0,1 kg dijatuhkan dari ketinggian 1,8 meter dan mengenai lantai. Kemudian dipantulkan kembali sampai ketinggian 1,2 m. Jika g = 10 m/s2. Tentukan :

A.    impuls karena berat bola ketika jatuh.

B.     koefisien restitusinya.

Jawab :

Besaran yang diketahui diketahui :

m = 0,1 kg

h = 1,8 m

h’ = 1,2 m

g = 10 m/s2

Selama bola jatuh ke tanah terjadi perubahan energi potensial menjadi energi kinetik, sehingga

Ep      = Ek

mgh   = ½ mv2

v        = √2gh

Impuls bola karena berat ketika jatuh adalah...

I   = F ∆t

    = m∆v

    = m√2gh

    = (0,1) √2(10) (1,8)

     = (0,1) (6)

             = 0,6 Ns

Koefisien restitusi:

       m = 0,1 kg

  h = 1,8 m

 h’ = 1,2 m

   g = 10 m/s2

e    = √h’ : h

= √1,2 : 1,8

= √2 : 3

= 0,8             

Contoh soal momentum

Dua bola masing- masing 2 kg. Bola pertama bergerak ke timur dengan kecepatan  4 m/s dan bola kedua bergerak keutara dengan kecepatan 3 m/s. Tentukan momentum total kedua benda tersebut.

Jawab :

Besaran yang diketahui :

m_A = 2 kg

m_B  = 2 kg

v_A  = 4 m/s

v_B  = 3 m/s

pA  = m.v = 2 kg . 4 m/s

      = 8 kg m/s

pB = m.v = 2 kg . 3 m/s

                   = 6 kg m/s

m_total= pA + pB

        = 8 kg m/s + 6 kg m/s

        = 14 kg  

BAB III

PENUTUP

3.1 Kesimpulan

Momentum adalah sebuah nilai dari perkalian materi yang bermassa / memiliki bobot dengan pergerakan / kecepatan. Dalam fisika momentum dilambangkan huruf ‘p’, secara matematis momentum dapat dirumuskan :

P= m.v

P = momentum, m = massa, v = kecepatan

Momentum akan berubah seiring dengan perubahan massa dan kecepatan. Semakin cepat pergerakan suatu materi/benda akan semakin cepat juga momentumnya. Semakin besar momentum, maka semakin dahsyat kekuatan yang dimiliki suatu benda. Jika materi dalam keadaan diam, maka momentumnya sama dengan nol. (filosofi : jika manusia tidak mau bergerak / malas, maka hasil kerjanya sama dengan nol).

Peristiwa – peristiwa yang terjadi sehari – hari erat kaitannya dengan momentum. salah satunya adalah tumbukan / tabrakan.

3.2. Saran

Dengan mengetahui dan mempelajari momentum, kita diharapkan dapat menganalisis apapun yang terjadi dalam kehidupan sehari – hari secara rasional. Momentum pula sangat banyak fungsinya dalam penggunaan berbagai alat yang berdaya guna dan bernilai dalam kehidupan. Jadi amatlah penting untuk mempelajari materi ini agar kita mengetahui asal muasal dari benda – benda yang kita pakai seperti yang disebutkan di atas.

DAFTAR PUSTAKA

Giacoli, Dougles C. 2001. Fisika JIlid 1. Jakarta : Erlangga.

Tippler, P.A. 1998. Fisika Untuk Sains dan Teknik. Jakarta : Erlangga.

 Hallyday dan Resnick. 1991. Fisika Jilid 1. Jakarta : Erlangga.

Young, Haug D. dan Freedman, Roger A. 2002. Fisika Universitas. Jakarta : Erlangga.

http://hartinhardiantins.blogspot.co.id/2013/11/makalah-impuls-dan-momentum.html

http://yefrytm.blogspot.co.id/2013/11/makalah-fisika-momentum-impuls-tumbukan.html

http://bpengertian.blogspot.com/2012/04/titik-berat-dan-pusat-masa-definisi.html#ixzz5AvmDKoWu

GHDSU

Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga

Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga

Halliday dan Resnick, 1991, FisiDNAKNDIka Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga

Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemaholi, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit ErlanggaGiancoli, Douglas C., 2001, Fisika Jilid I (terj

Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga

Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-

Share: